Semana 7 Encuestas

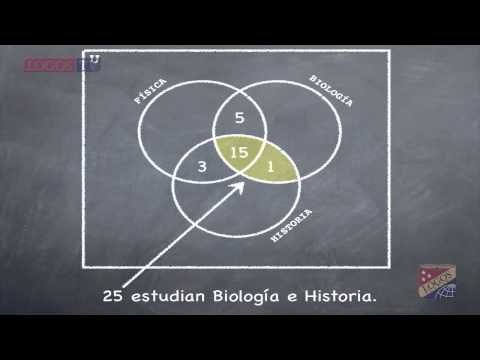
 SESIÓN 4 ENCUESTAS 

Esta fue la ultima clase y aprendimos a resolver problemas de encuestas y a resolver sudokus, lo ultimo me gustó y me pareció muy entretenido.

Semana 7 Producto cartesiano

 SESIÓN 2 PRODUCTO CARTESIANO 

Un conjunto puede contener pares ordenados como elementos. 

Si A y B son conjuntos, entonces cada elemento de A puede ser pareado con uno de B y así se obtienen los pares ordenados.

El conjunto con dichos pares se llama producto cartesiano de A y B, se escribe A x B.

A x B = {(a, b) / a ∈ A y b ∈ B}

Semana 7 Operación con conjuntos

 SESIÓN 1 OPERACIÓN CON CONJUNTOS 

 Operaciones con conjuntos.

Las operaciones con conjuntos también conocidas como álgebra de conjuntos, nos permiten realizar operaciones sobre los conjuntos para obtener otro conjunto. De las operaciones con conjuntos veremos las siguientes unión, intersección, diferencia, diferencia simétrica y complemento.

‒ Unión o reunión de conjuntos.

Es la operación que nos permite unir dos o más conjuntos para formar otro conjunto que contendrá a todos los elementos que queremos unir pero sin que se repitan. Es decir dado un conjunto A y un conjunto B, la unión de los conjuntos A y B será otro conjunto formado por todos los elementos de A, con todos los elementos de B sin repetir ningún elemento. El símbolo que se usa para indicar la operación de unión es el siguiente: ∪. Cuando usamos diagramas de Venn, para representar la unió de conjuntos, se sombrean los conjuntos que se unen o se forma uno nuevo. Luego se escribe por fuera la operación de unión.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5,6,7,} y B={8,9,10,11} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9,10,11}. Usando diagramas de Venn se tendría lo siguiente:

También se puede graficar del siguiente modo:

Ejemplo 2.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

Ejemplo 3.

Dados dos conjuntos F={x/x estudiantes que juegan fútbol} y B={x/x estudiantes que juegan básquet}, la unión será F∪B={x/x estudiantes que juegan fútbol o básquet}. Usando diagramas de Venn se tendría lo siguiente:

Ejemplo 4.

Dados los dos conjuntos A={3, 5, 6, 7} y B={5,6}, en donde B está incluido en A, la unión será AUB={3,5,6,7}. Usando diagramas de Venn se tendría

‒ Intersección de conjuntos.

Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la operación. Es decir dados dos conjuntos A y B, la de intersección de los conjuntos A y B, estará formado por los elementos de A y los elementos de B que sean comunes, los elementos no comunes A y B, será excluidos. El símbolo que se usa para indicar la operación de intersección es el siguiente: ∩.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la intersección de estos conjuntos será A∩B={4,5}. Usando diagramas de Venn se tendría lo siguiente:

Ejemplo 2.

Dados dos conjuntos A={x/x estudiantes que juegan fútbol} y B={x/x estudiantes que juegan básquet}, la intersección será F∩B={x/x estudiantes que juegan fútbol y básquet}. Usando diagramas de Venn se tendría lo siguiente:

‒ Diferencia de conjuntos.

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que pertenecen al primero pero no al segundo. Es decir dados dos conjuntos A y B, la diferencia de los conjuntos entra A y B, estará formado por todos los elementos de A que no pertenezcan a B. El símbolo que se usa para esta operación es el mismo que se usa para la resta o sustracción, que es el siguiente: -.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será A-B={1,2,3}. Usando diagramas de Venn se tendría lo siguiente:

‒ Diferencia de simetrica de conjuntos.

Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos. Es decir dados dos conjuntos A y B, la diferencia simétrica estará formado por todos los elementos no comunes a los conjuntos A y B. El símbolo que se usa para indicar la operación de diferencia simétrica es el siguiente: △.

Ejemplo 1.

Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:

 

Semana 6 Conjuntos: concentos, notación y formas de presentación

 SESIÓN 4 CONJUNTOS: CONCEPTOS, NOTACIÓN Y FORMAS DE PRESENTACIÓN 

Es posible representar gráficamente los conjuntos a través de diagramas de Venn.  Para trabajar con ellos es necesario poder representarlos también con el lenguaje propio de la matemática.

Se usan los corchetes  para representar y definir conjuntos.  En el interior de los corchetes se ubican los elementos que conforman el conjunto separados por comas.  Esta representación escrita es equivalente a la representación gráfica de diagramas de Venn.

Si por ejemplo se quiere definir el conjunto  como el conformado por los elementos , , , y  se puede representar de las siguientes formas:

Semana 6 Condicional. Negación de la condicional. Enunciados equivalentes a partir de la condicional

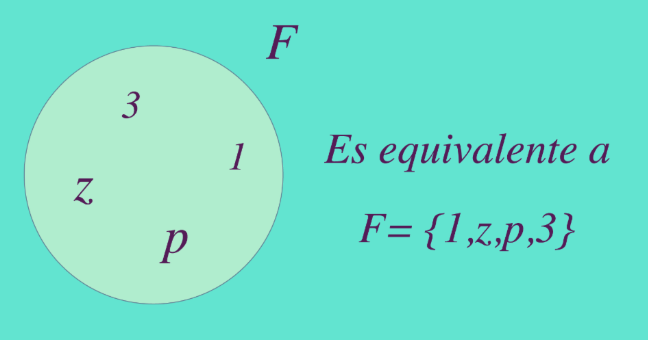
 SESIÓN 1 CONDICIONAL. NEGACIÓN DE LA CONDICIONAL Y ENUNCIADOS EQUIVALENTES A PARTIR DE LA CONDICIONAL. 

Semana 5 Proposiciones y tablas de verdad

 SESIÓN 2 PROPOSICIONES Y TABLAS DE VERDAD 

Una tabla de verdad de una proposición es un tablero que muestra todos los valores de verdad de un esquema molecular formada por todas las combinaciones posibles de las variables proposiciones que la componen. Valor de verdad de una proposición.

SESIÓN 3 CONJUNCIÓN Y DISYUNCIÓN 

SESIÓN 4 NEGACIÓN DE UNA PROPOSICIÓN COMPUESTA, LEYES DE MORGAN 

¿Qué son las leyes de De Morgan?

Las leyes de De Morgan son dos leyes lógicas pertenecientes a la lógica proposicional que fueron formuladas por el matemático inglés Augustus De Morgan (1806-1871). En ellas se establece lo siguiente, respecto a una proposición lógica compuesta:

1. El opuesto de una conjunción es equivalente a la disyunción que se forma con los opuestos o negaciones de las proposiciones que conforman la conjunción.
2. La negación de la disyunción se puede expresar como una conjunción conformada por los opuestos o negaciones de las proposiciones involucradas en la disyunción.

En la notación de la lógica proposicional, las leyes de De Morgan se expresan de una forma compacta y más formal así:

1. ∼(p ∧ q) ⇔ ∼p ∨ ∼q
2. ∼(p ∨ q) ⇔ ∼p ∧ ∼q

Semana 4 Interpretación de gráficas circulares y otro tipo de gráficas

 SESIÓN 3 INTERPRETACIÓN DE GRÁFICAS CIRCULARES 

En esta clase aprendimos a analizar gráficas, trabajamos en clase y esto fue algo de lo que hicimos.

Semana 4 Tangram y Ladrillos

 SESIÓN 1 TANGRAM

Esta sesión fue mi favorita, el Tangram es un juego chino que consiste en armar formas de animales o cosas con figuras geométricas, en otras palabras es un rompecabezas.

Ejemplo:

SESIÓN 2 LADRILLOS 

Los ladrillos son bastante similares al tangram porque tienes que armar figuras con cuadrados y rectángulos.

Ejemplo:

 

  

Semana 4 Ladrillos

 SESIÓN 2 LADRILLOS 

Semana 3 Estrategia plantear y resolver una ecuación

 SESIÓN 4 PLANTEAR Y RESOLVER UNA ECUACIÓN

La estrategia de utilizar una ecuación de primer grado para resolver un problema es muy importante, porque muchos problemas de las ciencias, la economía, las finanzas, la medicina y de otros campos se pueden plantear en términos de una ecuación. 

Ecuación Una ecuación es un enunciado que establece que dos expresiones son iguales, en ella se incluyen términos conocidos, variables o incógnitas y signos de operación y agrupación.

Semana 3 Estrategia proporciones y porcentajes

 SESIÓN 3 PROPORCIÓN Y PORCENTAJES 

Para el uso de esta estrategia necesitamos conocer ciertos conceptos fundamentales.

•  Razón Es el resultado de comparar dos cantidades y será siempre un número real. Sea la razón: 𝑥: 𝑦 (Se lee 𝑥 es a 𝑦) donde a 𝑥 le llamaremos antecedente, y a 𝑦 consecuente. 𝑥: 𝑦 = 𝑥 𝑦 = 𝑎𝑛𝑡𝑒𝑐𝑒𝑑𝑒𝑛𝑡𝑒 𝑐𝑜𝑛𝑠𝑒𝑐𝑢𝑒𝑛𝑡𝑒 Notemos que una razón es el cociente de dos cantidades.

 Ejemplo: 

3: 5 = 3 5 = 0.6 𝑒𝑙 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜 𝑒𝑠 𝑢𝑛 𝑛ú𝑚𝑒𝑟𝑜 𝑟𝑒𝑎𝑙 

• Proporción Se le denomina proporción a la igualdad de dos razones. Una proporción se puede escribir de las formas: 𝑎: 𝑏: 𝑐: 𝑑 que se lee: “𝑎 es a 𝑏 como 𝑐 es a 𝑑” 

Ejemplo:

2: 5 ∷ 4: 10 es equivalente a 2 5 = 4 10 Y leemos “2 es a 5 como 4 es a 10"

•  Porcentaje Un porcentaje es una razón en la cual el consecuente es 100. La razón representa un porcentaje y se puede escribir así: 𝑎𝑛𝑡𝑒𝑐𝑒𝑑𝑒𝑛𝑡𝑒 𝑐𝑜𝑛𝑠𝑒𝑐𝑢𝑒𝑛𝑡𝑒 = 𝑝 100 = 𝑝%

 Ejemplo: 

8 100 = 0.08 = 8% Propiedad de la igualdad de dos razones: 𝑎 𝑏 = 𝑐 𝑑 𝑎𝑑 = 𝑏𝑐

Ejemplo: 

Una empresa que fabrica tubos fluorescentes ofrece a sus clientes una garantía de 300 horas de vida útil para sus productos. ¿Cuál fue el porcentaje (¿%) de vida útil de un tubo fluorescente que duró 360 horas? 

Resolución del problema utilizando los cuatro pasos de Polya:

 1. Comprender el problema: ¿Qué debo encontrar? Se debe determinar el porcentaje (%) de vida útil del tubo fluorescente.

 2. Formular un plan: Para determinar el porcentaje (%), debemos formar una proporción que relacione las magnitudes.

 3. Llevar a cabo el plan: Procedemos a ejecutar el plan, formando la proporción y determinando el valor buscado. 

 Sea 𝒙 = 𝒑𝒐𝒓𝒄𝒆𝒏𝒕𝒂𝒋𝒆 𝒅𝒆 𝒗𝒊𝒅𝒂 ú𝒕𝒊𝒍 𝒅𝒆𝒍 𝒕𝒖𝒃𝒐 𝒇𝒍𝒖𝒐𝒓𝒆𝒔𝒄𝒆𝒏𝒕𝒆

𝑥/ 100 = 360/300 
𝑥 = 360 × 100/300
𝑥 = 120%

 Entonces el porcentaje de vida útil del tubo fluorescente es de 120%

 4. Revisar y comprobar: Esta comprobación se puede realizar sustituyendo la solución en la proporción original y verificando la igualdad.

 120/100 = 360/300
 120/300 = 1.2 = 360/300

Semana 3 Estrategia hacer un diagrama o figura

 SESIÓN 1 HACER UN DIAGRAMA O FIGURA 

En la mayoría de problemas es útil dibujar un diagrama o esquema, e identificar en él los datos e incógnitas del problema. En la figura se colocan todos los datos conocidos que da el problema y los datos que se pretenden encontrar, esto nos ayuda a tener una mejor idea y visualización de lo que el problema pide. 

Ejemplo: 

En una ferretería tienen un rollo  de 60m de alambre, y diario cortan 10m. ¿En cuántos días habrán cortado todo el alambre?

1.  Entender el problema: determinar en cuántos días habrán terminado el rollo de alambre de 60m, si a diario cortan 10m.
2.   Formular un plan: Mediante un gráfico demostrar la disminución del alambre día con día,
3.   Ejecutar el plan:

En la primer barra del gráfico se demuestra la cantidad total del rollo de alambre y seguido se grafica cómo cada día disminuyen 10m del total del alambre; consiguiendo de esta manera que el alambre se agote en 6 días.